| HIFI-FORUM » Stereo » Elektronik » Analogtechnik/Plattenspieler » Effektive Tonarmmasse | |
|
|
||||
Effektive Tonarmmasse+A -A |
||
| Autor |
| |
|
Beaufighter
Inventar |
#1
erstellt: 22. Nov 2013, 14:52

|
|
|
Moin moin, seit längerem beschäftigt mich das Thema wie man die Tonarmmasse selber berechnen könnte. Ich habe mal ein einfaches Modell erstellt anhand dessen ich gerne mal den Steinerschen Satz nachfollzogen hätte.  Wie wendet man nun diese Formel darauf an?
Gruß Beaufighter [Beitrag von Beaufighter am 22. Nov 2013, 14:56 bearbeitet] |
||
|
Beaufighter
Inventar |
#2
erstellt: 22. Nov 2013, 15:20

|
|
|
So nun noch mal hinterher hoffe das kommt hin... 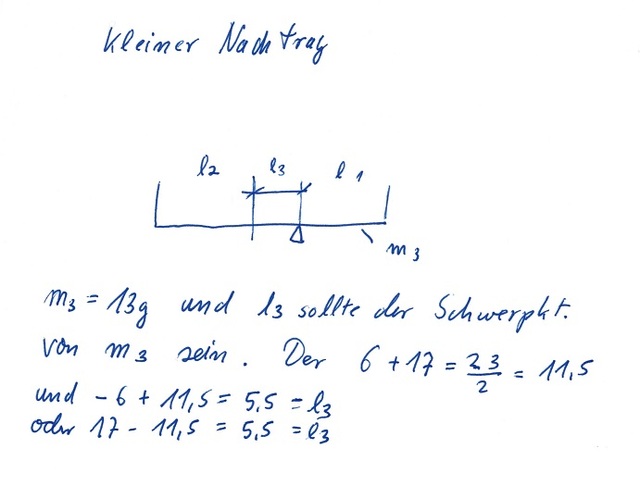 Dabei gehe ich in diesem Fall von einem homogenen Tonarmrohr aus welches pro laufendem cm (13/23) Gramm wiegt. Gruß [Beitrag von Beaufighter am 22. Nov 2013, 15:24 bearbeitet] |
||
|
|
||
|
Gelscht
Gelöscht |
#3
erstellt: 22. Nov 2013, 16:43

|
|
|
Was ist jetzt genau Deine Frage? Von dem, was ich aus Deinen beiden Beiträgen verstehe, würde ich sagen: Das geht so nicht. Der Steinersche Satz hilft doch nur, wenn das bereits bekannte Trägheitsmoment für die Achse durch den Schwerpunkt für eine verschobene Achse berechnet werden soll. Für das Tonarmrohr müsstest Du also dieses Trägheitsmoment bereits kennen. Ansonsten: Die eff. Masse des Tonarms wird berechnet, in dem das Trägheitsmoment durch das Quadrat der eff. Tonarmlänge geteilt wird. Gruß Thomas |
||
|
juergen1
Inventar |
#4
erstellt: 22. Nov 2013, 16:53

|
|
|
"Es werden zuerst die einzelnen Trägheitsmomente O n der verschiedenen Einzelmassen bestimmt: Armrohr, Headshell...... Diese Momente werden aufsummiert. Das resultierende Gesamtmoment wird durch den Abstand Lm (Armlager – Auflagepunkt) geteilt und ergibt so die effektive Masse des Arms.“ Hallo Beaufighter, auf Anhieb hätte ich jetzt gesagt, das ist falsch. Und man müßte das Gesamtträgeitsmoment durch das Quadrat des Abstands (Nadel -Tonarmlager) teilen. So wie Du ja auch vermutest. Ein Gewicht direkt über der Nadel geht ja 1:1 in die effektive Masse ein, soweit ich erinnere. Und das funktioniert nicht, wenn man erst mit dem Quadrat der effektiven Länge multipliziert und dann durch die einfache effektive Länge wieder teilt. Obiger Satz würde stimmen, wenn es sich um Drehmomente handeln würde... Gruß Jürgen |
||
|
juergen1
Inventar |
#5
erstellt: 22. Nov 2013, 16:56

|
|
|
||
|
Beaufighter
Inventar |
#6
erstellt: 22. Nov 2013, 16:56

|
|
|
Na ich dachte ich habe 3 Massenträgheitsmomente die ich dann zu einem für den gesamten Tonarm bringen muß. Also einmal das Tonarmrohr, einmal das Gegengewicht und einmal das Headshell. Daraus könnte man doch irgendwie die effektive Masse dieses Tonarms bestimmen oder ? |
||
|
Beaufighter
Inventar |
#7
erstellt: 22. Nov 2013, 17:31

|
|
|
Dan fehlt zur Berrechnung noch die effektive Tonarmläge? |
||
|
Gelscht
Gelöscht |
#8
erstellt: 22. Nov 2013, 17:35

|
|
Woher hast Du die? Headshell/System und Gegengewicht kannst Du ja näherungsweise mit m*d^2 abschätzen. Aber für das Armrohr hast Du nur die gleichmäßig verteilte Masse und eben nicht das Trägheitsmoment. Das müsstest Du erstmal berechnen:  Hauptträgheitsmomente einfacher geometrischer Körper Hauptträgheitsmomente einfacher geometrischer Körperf) Ein Zylindermantel, der um eine Querachse (zweizählige Symmetrieachse) rotiert. Danach kannst Du mit dem Steinerschen Satz das Trägheitsmoment des Tonarmrohr mit der Achse im Tonarmlager berechnen. Gruß Thomas |
||
|
Beaufighter
Inventar |
#9
erstellt: 22. Nov 2013, 17:40

|
|
|
Nun ja ich hab den Drehpunkt des Tonarmrohres und ich hab den Schwerpunkt der 5,5 cm vom Drehpunkt entfernt ist. Es geht nur um diesen fiktiven Tonarm. |
||
|
juergen1
Inventar |
#10
erstellt: 22. Nov 2013, 18:26

|
|
Und genaugenommen darfst Du für die Ermittlung der einzelnen Trägheitsmomente nicht einfach mit dem Abstand Masseschwerpunkt der einzelnen Gewichte zum Lager rechnen. Das funktioniert nur beim Drehmoment, nicht aber beim Trägheitsmoment. Bei Wiki findest Du unter "Trägheitsmoment" die Formeln für einfache geometrische Formen wie Rohr oder Stab. Für einen Stab gilt bspw.: Trägheitsmoment =1/3 Masse mal Länge^2 Und nicht etwa: Masse mal halbe Länge, wie man fürs Drehmoment rechnen wüde. Das reicht zur Annäherung. Für ganz exakte Berechnung komplizierter Formen bräuchtes Du ein 3-D CAD-Programm, welches die Werte auf Knopfdruck ausspuckt. Gruß Jürgen [Beitrag von juergen1 am 22. Nov 2013, 18:34 bearbeitet] |
||
|
juergen1
Inventar |
#11
erstellt: 22. Nov 2013, 18:39

|
|
|
||
|
Beaufighter
Inventar |
#12
erstellt: 22. Nov 2013, 19:19

|
|
|
Warum? |
||
|
juergen1
Inventar |
#13
erstellt: 22. Nov 2013, 19:48

|
|
|
||
|
Beaufighter
Inventar |
#14
erstellt: 22. Nov 2013, 20:28

|
|
|
Dann ist es auf diese Art und Weise nicht möglich die effektive Masse dieses Tonarms zu bestimmen? |
||
|
Beaufighter
Inventar |
#15
erstellt: 22. Nov 2013, 20:47

|
|
|
Aber sobald ich meine Massen anders Verteile ändert sich doch auch der Schwerpunkt .....  Das hängt doch kausal zusammen. Da sollte es doch einen mathematischen Zusammenhang geben? |
||
|
juergen1
Inventar |
#16
erstellt: 23. Nov 2013, 00:38

|
|
Gruß Jürgen |
||
|
juergen1
Inventar |
#17
erstellt: 23. Nov 2013, 00:40

|
|
|
||
|
tomtiger
Administrator |
#18
erstellt: 23. Nov 2013, 10:49

|
|
|
Hi, ich habe nicht nachgerechnet, aber mE. muss man den Tonarm als Ganzes betrachten. Hat man das Trägheitsmoment des ganzen Tonarms und dessen Schwerpunkt, kann man den Steinerschen Satz anwenden. Die Zerlegung eines unregelmässig geformten Körpers in einzelne einfache geometrische Körper und der Summierung deren Trägheitsmomente ist mE. nicht so einfach möglich. LG Tom |
||
|
Gelscht
Gelöscht |
#19
erstellt: 23. Nov 2013, 12:00

|
|
Trägheitsmomente mit der gleichen Achse kann man einfach addieren. Hat man die Trägheitsmomente nicht für die gleichen Achsen, sondern jeweils für die Achsen durch den Schwerpunkt der einzelnen Komponenten, kann man die Achsen verschieben (und so gleich machen), das Trägheitsmoment der einzelnen Komponenten mit dem Steinerschen Satz neu berechnen und danach addieren. Ursprünglich war ich davon ausgegangen, dass Beaufighter das plant. Was er vorhat, ist allerdings physikalisch falsch. Gruß Thomas |
||
|
Beaufighter
Inventar |
#20
erstellt: 23. Nov 2013, 18:59

|
|
|
Naja, das war nur ein Ansatz von mir. Ich freue mich wenn meine Fehler aufgezeigt werden. Mein Ziel ist es eine richtige Lösung wenn es geht mit Euch zu finden.  Ich bin kein Physiker und auch kein Mathematiker, ich will nur endlich mal wissen wie man Bsp. ein einfaches Modell von Tonarm berechnen kann. Das würde ich spannend finden. Gruß Beaufighter |
||
|
juergen1
Inventar |
#21
erstellt: 23. Nov 2013, 19:53

|
|
|
Mal doch mal eine ganz einfache Skizze mit einem ansonsten gewichtslosen Tonarm, bei dem einzig der Tonabnehmer eine Masse hat. Mit den Abstandsmaßen Vorderkante und Hinterkante des Tonabnehmers vom Lager. Und seinem Gewicht. Und natürlich auch Abstand der Nadel vom Lager. Daran kann man das Prinzip erläutern. Es ist eigentlich sehr einfach. Gruß Jürgen |
||
| ||
|
|
||||
| Das könnte Dich auch interessieren: |
|
Wie die effektive Tonarmmasse bestimmen? Hupert am 08.08.2008 – Letzte Antwort am 10.08.2008 – 6 Beiträge |
|
effektive Tonarmmasse? Arminschen am 19.01.2004 – Letzte Antwort am 28.05.2004 – 22 Beiträge |
|
Effektive Tonarmmasse SaschaK am 28.10.2004 – Letzte Antwort am 18.11.2004 – 15 Beiträge |
|
Moerch UP4 effektive Tonarmmasse Isophon2011 am 29.01.2011 – Letzte Antwort am 30.01.2011 – 8 Beiträge |
|
Effektive Tonarmmasse Technics ps310 am 16.08.2016 – Letzte Antwort am 22.12.2016 – 12 Beiträge |
|
Effektive Tonarmmasse erhöhen d0um am 02.04.2010 – Letzte Antwort am 09.04.2010 – 41 Beiträge |
|
Effektive Tonarmmasse Dual 701 Keksstein am 21.12.2018 – Letzte Antwort am 22.12.2018 – 6 Beiträge |
|
effektive Tonarmmasse erhöhen? Bernd am 16.11.2003 – Letzte Antwort am 17.11.2003 – 5 Beiträge |
|
SME 3009R effektive Tonarmmasse ? stereoplay am 17.10.2007 – Letzte Antwort am 18.10.2007 – 6 Beiträge |
|
Technics SL -1200 GR Effektive Tonarmmasse Beaufighter am 24.10.2020 – Letzte Antwort am 27.10.2020 – 10 Beiträge |
Foren Archiv
2013
Anzeige
Produkte in diesem Thread

Aktuelle Aktion
Top 10 Threads in Analogtechnik/Plattenspieler der letzten 7 Tage

- Plattengewicht Ja oder Nein
- Nadel rutscht beim Aufsetzen sofort nach innen (AS und AL korrekt eingestellt!)
- Plattenspieler Setup + Sonos möglich?
- Braun PS 500 - Läuft nicht an
- elliptisch, sphärisch, hä?
- Hilfe: Plattenteller eiert
- Nadel / Tonkopf für einen Sharp RP-1500H
- Dual 1019 - wie gut ist der?
- Frage zu Strobe Beleuchtung an Plattenspielern
- s-laute ,scharf,aggressiv,zischelnd-- warum?
Top 10 Threads in Analogtechnik/Plattenspieler der letzten 50 Tage

- Plattengewicht Ja oder Nein
- Nadel rutscht beim Aufsetzen sofort nach innen (AS und AL korrekt eingestellt!)
- Plattenspieler Setup + Sonos möglich?
- Braun PS 500 - Läuft nicht an
- elliptisch, sphärisch, hä?
- Hilfe: Plattenteller eiert
- Nadel / Tonkopf für einen Sharp RP-1500H
- Dual 1019 - wie gut ist der?
- Frage zu Strobe Beleuchtung an Plattenspielern
- s-laute ,scharf,aggressiv,zischelnd-- warum?
Top 10 Suchanfragen

Forumsstatistik

- Registrierte Mitglieder930.911 ( Heute: 1 )
- Neuestes Mitglieddenisewill
- Gesamtzahl an Themen1.564.143
- Gesamtzahl an Beiträgen21.844.713